v
MEDIAN
Pada data tunggal, penghitungan median cukup mudah.
Data diurutkan berdasarkan nilai datanya mulai dari yang terkecil sampai yang
terbesar. Kemudian median bisa diketahui langsung dari nilai tengah urutan data
tersebut.
Namun pada data berkelompok, cara tersebut tidak bisa digunakan. Data berkelompok merupakan data yang berbentuk kelas interval, sehingga kita tidak bisa langsung mengetahui nilai median jika kelas mediannya sudah diketahui.
Namun pada data berkelompok, cara tersebut tidak bisa digunakan. Data berkelompok merupakan data yang berbentuk kelas interval, sehingga kita tidak bisa langsung mengetahui nilai median jika kelas mediannya sudah diketahui.
Oleh karena itu, kita harus menggunakan rumus berikut ini.

Me = median
xii =
batas bawah median
n = jumlah data
fkii = frekuensi kumulatif
data di bawah kelas median
fi = frekuensi data pada
kelas median
p = panjang interval kelas
Contoh Soal No. 1
Sebanyak 26 orang mahasiswa terpilih sebagai sampel
dalam penelitian kesehatan di sebuah universitas. Mahasiswa yang terpilih
tersebut diukur berat badannya. Hasil pengukuran berat badan disajikan dalam
bentuk data berkelompok seperti di bawah ini.

Hitunglah median berat badan mahasiswa!
Jawab:
Sebelum menggunakan rumus di atas, terlebih dahulu
dibuat tabel untuk menghitung frekuensi kumulatif data. Tabelnya adalah sebagai
berikut.

Selanjutnya adalah menentukan nilai-nilai yang akan
digunakan pada rumus.
Jumlah data adalah 26, sehingga mediannya terletak
di antara data ke 13 dan 14. Data ke-13 dan 14 ini berada pada kelas interval
ke-4 (61 – 65). Kelas interval ke-4 ini kita sebut kelas median.
Melalui informasi kelas median, bisa kita peroleh
batas bawah kelas median sama dengan 60,5. Frekuensi kumulatif sebelum kelas
median adalah 9, dan frekuensi kelas median sama dengan 5. Diketahui juga,
bahwa panjang kelas sama dengan 5.
Secara matematis bisa diringkas sebagai berikut:
xii =
60,5
n = 26
fkii = 9
fi = 5
p = 5
Dari nilai-nilai tersebut dapat kita hitung median
dengan menggunakan rumus median data berkelompok.

Sehingga median berat badan mahasiswa adalah 64,5
kg.
v MODUS
Rumus Modus Data Kelompok
Pengertian modus adalah
nilai data yang paling sering muncul atau data yang mempunyai nilai frekuensi
paling tinggi. Cara mencari nilai modus pada data tunggal sangat mudah, sobat
idschool hanya perlu mencari data dengan frekuensi paling banyak.
Cara mencari nilai modus
data kelompok tidak semudah mencari nilai modus pada data tunggal. Hal ini
dikarenakan penyajian data kelompok yang disajikan dalam sebuah rentang kelas.
Sehingga, nilai modus data kelompok tidak mudah untuk langsung didapat.
Untuk mendapatkan nilai modus data kelompok dapat
menggunakan sebuah rumus. Rumus modus data kelompok dapat dilihat seperti
persamaan di bawah.

Keterangan:
Tb = tepi bawah kelas modus
d1 = selisih frekuensi kelas modus dengan
frekuensi sebelum kelas modus
d2 = selisih frekuensi kelas modus dengan
frekuensi setelah kelas modus
p = panjang kelas interval
Contoh 1:
soal dan pembahasan modus pada data kelompok.
Perhatikan gambar diagram
batang di bawah!

Modus dari data yang
disajikan pada diagram batang di atas adalah ….
A. 46,0
B. 46,5
C. 47,0
D. 49,0
E. 49,5
B. 46,5
C. 47,0
D. 49,0
E. 49,5
Pembahasan:
Dari diagram diketahui modus ada pada interval 45 – 49, sehingga Maka
nilai Modus (Mo) dari data tersebut adalah:
Jawaban: B
v
MEAN
Rumus Mean (Rata-rata) Data Kelompok
Inti dari menentukan nilai
rata-rata dari suatu data kelompok sama dengan mencari nilai rata-rata data
tunggal. Idenya adalah menjumlahkan semua data kemudian membagi dengan
banyaknyanya data. Hanya saja, karena penyajian data kelompok diberikan dalam
bentuk berbeda, maka rumus mencari nilai mean untuk data kelompok sedikit
berbeda dengan cara mencari nilai mean pada data tunggal.
Rumus mean data kelompok dinyatakan
dalam persamaan di bawah.

Keterangan:
= rataan hitung dari
data kelompok
fi = frekuensi kelas ke-i
xi = nilai tengah kelas ke-i
Contoh 1: soal dan pembahasan cara mencari nilai median pada data kelompok.
Perhatikan data pada tabel
berikut!

Nilai mean (rata-rata) dari
data pada tabel tersebut adalah ….
A.60,75
B.61,75
C.62,75
D.63,75
E.64,75
B.61,75
C.62,75
D.63,75
E.64,75
Pembahasan:
Untuk menentukan rata-rata
dari suatu kelompok, kita membutuhkan nilai tengah dari masing-masing kelas.
Nilai tengah dari masing-masing kelas dapat diperoleh menggunanan rumus
berikut.

Nilai tengah masing-masing kelas adalah sebagai berikut.
Hasil perkalian nilai
tengah masing-masing kelas dan frekuensinya dapat dilihat pada tabel di bawah.

Sehingga

Jadi, nilai mean dari data
yang diberikan pada soal adalah 61,75.
Jawaban: B
v
KUARTIL, DESIL, DAN PERSENTIL
Mencari Nilai Kuartil Untuk Data Tunggal
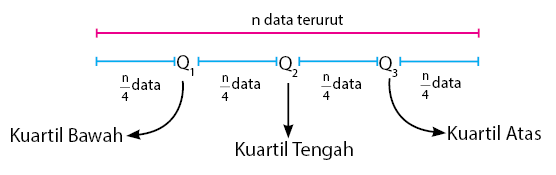
Seperti yang telah disebutkan sebelumnya, kuartil
membagi data menjadi empat bagian sama banyak. Sehingga terdapat tiga nilai
kuartil yang membagi data tersebut. Sebelum membagi data, pastikan bahwa data
sudah diurutkan terlebih dahulu. Ilustrasinya dapat dilihat seperti gambar di
bawah.
Rumus mencari nilai kuartil untuk data tunggal
dibedakan menjadi dua kasus, yaitu untuk jumah data ganjil dan jumlah data
genap.
Untuk n ganjil:

Untuk n genap:
Langkah-langkah mencari tiga nilai kuartil data
tunggal untuk jumlah data genap adalah sebagai berikut.
1.
Carilah nilai yang menjadi nilai tengah (median atau Q2).
2.
Membagi data di sebelah kiri median menjadi dua bagian yang sama
dan menghasilkan kuartil bawah atau Q1.
3.
Membagi data di sebelah kanan median menjadi dua bagian sama dan
menghasilkan kuartil atas atau Q3.
Berikutnya adalah ulasan materi tentang desil.
Mencari Nilai Desil Untuk Data Tunggal
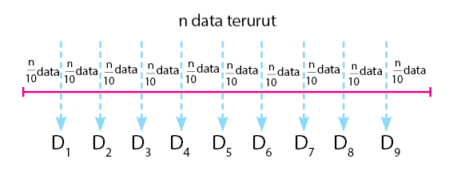
Desil adalah cara membagi n data terurut menjadi 10
bagian data yang masing-masing bagian mempunyai jumlah data yang sama. Setiap n
data terurut dibagi menjadi 10 bagian, sehingga terdapat 9 nilai desil.
Ilustrasi pembagian n data terurut menjadi 10 bagian sama banyak dan letak
nilai desilnya dapat dilihat pada gambar di bawah.
Rumus desil dinyatakan dalam persamaan di bawah.

Keterangan:
i = bilangan bulat kurang dari 10 (1, 2, 3, …, 9)
n = banyak data
n = banyak data
Mencari Nilai Persentil Untuk Data Tunggal
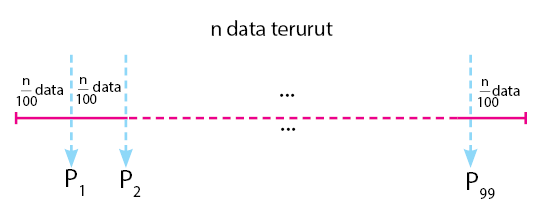
Persentil diambil dari kata persen, per seratus.
Sehingga, persentil merupakan pembagian n data terurut menjadi 100 bagian sama
banyak. Dari 100 bagian yang dibagi sama banyak tersebut, dibatasi oleh 99
nilai persentil. Perhatikan ilustrasi pembagian data dan letak nilai persentil
seperti gambar di bawah.
Rumus persentil data tunggal di berikan seperti
persamaan di bawah.

Keterangan:
i = bilangan bulat kurang dari 100 (1, 2, 3, …, 99)
n = banyak data
n = banyak data
Pembahasan selanjutnya adalah rumus kuartil, desil,
dan persentil pada data kelompok.
Rumus Kuartil, Desil,
dan Persentil Data Kelompok
Seperti halnya data tunggal, data yang telah
disajikan menjadi data kelompok juga dapat dicari nilai kuartil, desil, dan
persentilnya. Rumus kuartil, desil, dan persentil data kelompok berbeda dengan
rumus kuartil, desil, dan pesentil untuk data tunggal. Meskipun begitu, ide dan
pengertian kuartil, desil, dan persentil pada data kelompok sama dengan pada
data tunggal.
Berikut ini adalah rumus
kuartil, desil, dan persentil untuk data kelompok.
Rumus Kuartil Data Kelompok
Terdapat tiga nilai kuartil pada data kelompok, yaitu
kuartil bawah, kuartil tengah, dan kuartil atas. Rumus kuartil data kelompok
diberikan seperti persamaan di bawah.
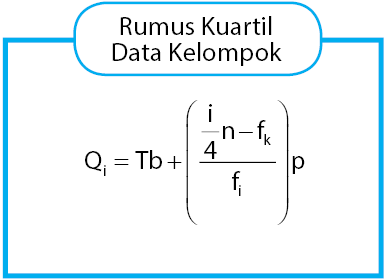
Keterangan:
i = 1 untuk kuartil
bawah
i = 2 untuk kuartil tengah
i = 3 untuk kuartil atas
Tb = tepi bawah kelas kuartil
n = jumlah seluruh frekuensi
fk = jumlah frekuensi sebelum kelas kuartil
fi = frekuensi kelas kuartil
p = panjang kelas interval
i = 2 untuk kuartil tengah
i = 3 untuk kuartil atas
Tb = tepi bawah kelas kuartil
n = jumlah seluruh frekuensi
fk = jumlah frekuensi sebelum kelas kuartil
fi = frekuensi kelas kuartil
p = panjang kelas interval
Rumus Desil Data Kelompok
Cara mencari nilai desil pada data kelompok dapat
menggunakan rumus desil untuk data kelompok yang diberikan di bawah.

Keterangan:
i = bilangan bulat
kurang dari 10 (1, 2, 3, … ,9)
Tb = tepi bawah kelas desil
n = jumlah seluruh frekuensi
fk = jumlah frekuensi sebelum kelas desil
fi = frekuensi kelas desil
p = panjang kelas interval
Tb = tepi bawah kelas desil
n = jumlah seluruh frekuensi
fk = jumlah frekuensi sebelum kelas desil
fi = frekuensi kelas desil
p = panjang kelas interval
Rumus Persentil Data Kelompok
Rumus persentil data kelompok digunakan untuk
menentukan nilai persentil dari suatu data kelompok. Rumus tersebut ditunjukkan
seperti persamaan di bawah.

Keterangan:
i = bilangan bulat
kurang dari 100 (1, 2, 3, … ,99)
Tb = tepi bawah kelas persentil
n = jumlah seluruh frekuensi
fk = jumlah frekuensi sebelum kelas persentil
fi = frekuensi kelas persentil
p = panjang kelas interval
Tb = tepi bawah kelas persentil
n = jumlah seluruh frekuensi
fk = jumlah frekuensi sebelum kelas persentil
fi = frekuensi kelas persentil
p = panjang kelas interval
Untuk menambah
pemahaman sobat idschool tentang materi rumus kuartil, desil, dan persentil
akan diberikan contoh
soal kuartil, desil, dan persentil beserta cara menyelesaikan
menggunakan rumus-rumus yang telah diberikan di atas.
Contoh Soal dan Pembahasan
Contoh Soal Kuartil Data
Tunggal
Perhatikan data nilai matematika yang diperoleh
sekelompok siswa berikut.

Nilai kuartil bawah pada data yang
diberikan di atas adalah ….
A. 49
B. 52
C. 55
D. 59
E. 68
B. 52
C. 55
D. 59
E. 68
Pembahasan:
Langkah pertama yang dilakukan adalah mengurutkan
data dan mencari nilai mediannya. Data yang telah diurutkan dan nilai median
dapat dilihat pada gambar di bawah.

Selanjutnya, mencari nilai kuartil bawahnya , diperoleh dari nilai tengah dari
data terurut di sebelah kiri median.
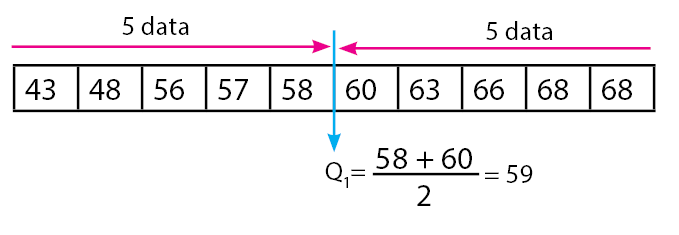
Jadi, nilai kuartil bawahnya adalah 59
Jawaban: D
DAFTAR
PUSTAKA